Catalan Numbers

The Catalan numbers (1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, ...), named after Eugène Charles Catalan (1814–1894), arise in a number of problems in combinatorics. They can be computed using this formula:

Among other things, the Catalan numbers describe:

• the number of ways a polygon with n+2 sides can be cut into n triangles
• the number of ways to use n rectangles to tile a stairstep shape (1, 2, ..., n−1, n).
• the number of ways in which parentheses can be placed in a sequence of numbers to be multiplied, two at a time
• the number of planar binary trees with n+1 leaves
• the number of paths of length 2n through an n-by-n grid that do not fall below the main diagonal

The following figures show some of the interpretations—polygon divisions, binary trees, pairwise multiplication—combined. For n=2:

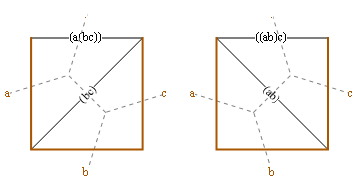
And n=3:

Polygon diagrams:

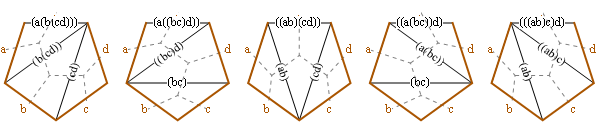
4 sides, 2 ways:

5 sides, 5 ways:

6 sides, 14 ways:

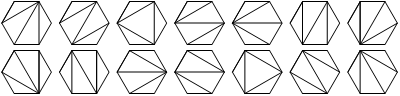
7 sides, 42 ways:

8 sides, 132 ways:

9 sides, 429 ways:
(Hidden in file catalan9.png, as we used to do.)

Step diagrams:

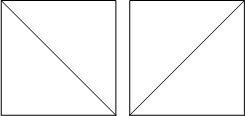
2 rectangles, 2 ways:

3 rectangles, 5 ways:

4 rectangles, 14 ways:

5 rectangles, 42 ways:

6 rectangles, 132 ways:

Multiplication diagrams:

3 numbers:

(1 (2 3))   ((1 2) 3)

4 numbers:

(1 (2 (3 4)))   (1 ((2 3) 4))
((1 2) (3 4))   ((1 (2 3)) 4)
(((1 2) 3) 4)

5 numbers:

(1 (2 (3 (4 5))))   (1 (2 ((3 4) 5)))
(1 ((2 3) (4 5)))   (1 ((2 (3 4)) 5))
(1 (((2 3) 4) 5))   ((1 2) (3 (4 5)))
((1 2) ((3 4) 5))   ((1 (2 3)) (4 5))
((1 (2 (3 4))) 5)   ((1 ((2 3) 4)) 5)
(((1 2) 3) (4 5))   (((1 2) (3 4)) 5)
(((1 (2 3)) 4) 5)   ((((1 2) 3) 4) 5)

6 numbers:

(1 (2 (3 (4 (5 6)))))   (1 (2 (3 ((4 5) 6))))
(1 (2 ((3 4) (5 6))))   (1 (2 ((3 (4 5)) 6)))
(1 (2 (((3 4) 5) 6)))   (1 ((2 3) (4 (5 6))))
(1 ((2 3) ((4 5) 6)))   (1 ((2 (3 4)) (5 6)))
(1 ((2 (3 (4 5))) 6))   (1 ((2 ((3 4) 5)) 6))
(1 (((2 3) 4) (5 6)))   (1 (((2 3) (4 5)) 6))
(1 (((2 (3 4)) 5) 6))   (1 ((((2 3) 4) 5) 6))
((1 2) (3 (4 (5 6))))   ((1 2) (3 ((4 5) 6)))
((1 2) ((3 4) (5 6)))   ((1 2) ((3 (4 5)) 6))
((1 2) (((3 4) 5) 6))   ((1 (2 3)) (4 (5 6)))
((1 (2 3)) ((4 5) 6))   ((1 (2 (3 4))) (5 6))
((1 (2 (3 (4 5)))) 6)   ((1 (2 ((3 4) 5))) 6)
((1 ((2 3) 4)) (5 6))   ((1 ((2 3) (4 5))) 6)
((1 ((2 (3 4)) 5)) 6)   ((1 (((2 3) 4) 5)) 6)
(((1 2) 3) (4 (5 6)))   (((1 2) 3) ((4 5) 6))
(((1 2) (3 4)) (5 6))   (((1 2) (3 (4 5))) 6)
(((1 2) ((3 4) 5)) 6)   (((1 (2 3)) 4) (5 6))
(((1 (2 3)) (4 5)) 6)   (((1 (2 (3 4))) 5) 6)
(((1 ((2 3) 4)) 5) 6)   ((((1 2) 3) 4) (5 6))
((((1 2) 3) (4 5)) 6)   ((((1 2) (3 4)) 5) 6)
((((1 (2 3)) 4) 5) 6)   (((((1 2) 3) 4) 5) 6)

Tree diagrams:

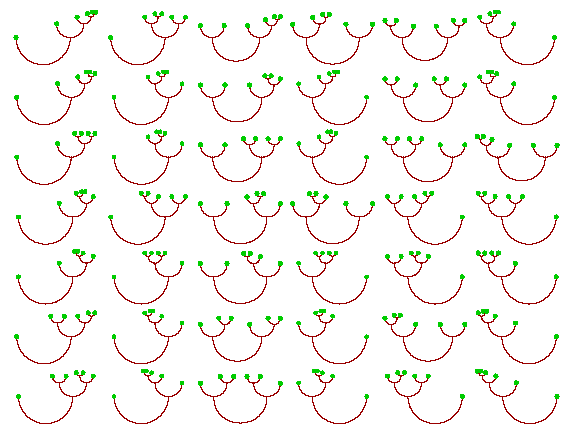
3 nodes:

4 nodes:

5 nodes:

6 nodes:

Path diagrams:

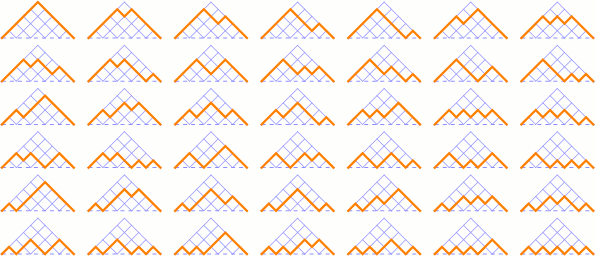
2 × 2 grid:

3 × 3 grid:

4 × 4 grid:

5 × 5 grid:

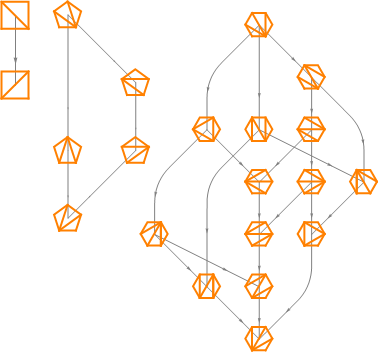
The Catalan interpretations can be partially ordered and arranged into a lattice called a Tamari lattice:

You might also enjoy the generalization Fuss–Catalan numbers.

Originally designed and rendered using Mathematica 3.0 for the Apple Macintosh.

Inspiration and facts (though not figures) by Brian Hayes, “A Question of Numbers” [dead link], American Scientist, January–February 1996; Steven S. Skiena, Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica, Addison-Wesley, 1990; Fred S. Roberts, Applied Combinatorics, Prentice-Hall, 1984; D. E. Knuth, Sorting and Searching (vol. 3 of The Art of Computer Programming), Addison-Wesley, 1973. Catalan dates from Florian Cajori, A History of Mathematics, The Macmillan Company, 1922; R. P. Stanley, Enumerative Combinatorics, Volume 2, Cambridge: Cambridge University Press, 1999.

See also Martin Gardner, Time Travel and Other Mathematical Bewilderments, Chapter 20, W. H. Freeman, 1988; and Ilan Vardi, Computational Recreations in Mathematica, Chapter 9, Addison-Wesley, 1991.

© 1996–2024 by Robert Dickau.

[ home ] || [ 2011-02-27 ]