There are 2 self-avoiding (non-self-intersecting) paths from the southwest corner of a grid back to the beginning, using only steps north, east, south, or west, that stay within a 1 × 1 grid:
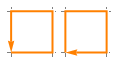
(If you don’t care about orientation, you can divide each total by two.)
This kind of thing is sometimes called a self-avoiding polygon.
14 self-avoiding paths through a 2 × 2 grid back to the beginning:
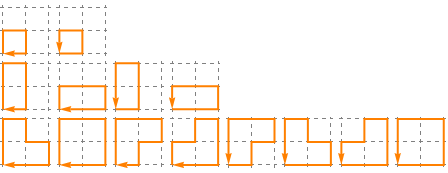
(Of these 14 paths: the first 2 take 4 steps; the next 4 paths take 6 steps; and the last 8 paths take 8 steps.)
194 paths through a 3 × 3 grid back to the beginning:

(Of these 194 paths: 2 of them take 4 steps; 4 take 6 steps; 12 take 8 steps; 36 take 10 steps; 80 take 12 steps; 48 take 14 steps; and 12 take 16 steps.)
Let’s not concern ourselves with the 8,222 self-avoiding loops through a 4 × 4 grid.
Of course, this isn’t the full set of self-avoiding polygons, since points other than the corners can be used as the start and end.
While we’re on the subject, there seem to be 42 self-avoiding paths through a 1 × 1 × 1 lattice:
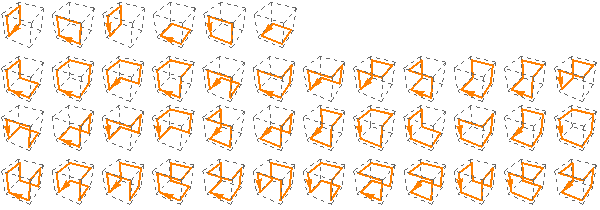
(Of these 42 paths: 6 of them take 4 steps; 24 paths take 6 steps; and 12 paths take 8 steps.)
© 2011–2026 by Robert Dickau.
[ home ] || [ 2012-03-31 ]