
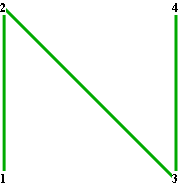
Begin with an N shape made by connecting four points at the corners of a square like this:

Next, make a copy of the whole figure at each corner of the N shape:
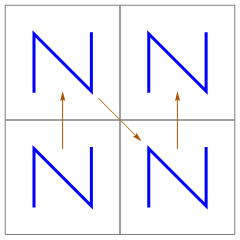
Finally, connect the last point of one figure with the first point of the next, where “last”, “first”, and “next” are relative to the initial order of the points:
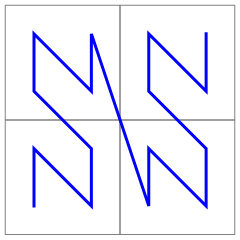
Repeating the process generates a non-self-intersecting, plane-filling curve called the Lebesgue curve:




(I must be doing this sideways, since some references call this the z-order curve.)
The Lebesgue curve maps (one-dimensional) integers to (two-dimensional) points in a square:
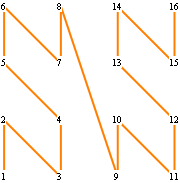

Of course, there are other ways to connect the initial four points and to arrange subsequent figures. The following figures show the evolution of quasi-Lebesgue curves generated by the other possible arrangements.
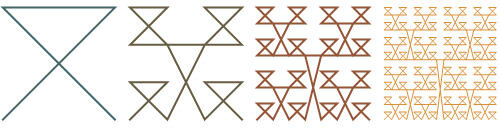
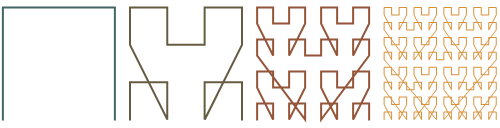
Alas, randomizing the order of arrangements at each step doesn’t seem that interesting, either:
You might enjoy the 3D version of the same thing.
See, for example, Hans Sagan, Space-Filling Curves, Universitext, 1994, pp. 76–80.
Figures created with Mathematica 6.
© 2008–2026 Robert Dickau.
[ home ] || [ 2008-05-04 ]
www.robertdickau.com/lebesgue2d.html