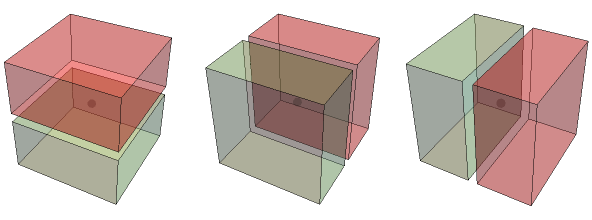
Here’s a 3D analog to 2D Schröder rectangulations, also called 3D guillotine partitions.
1 slice, 3 ways:

(The ghostly dots are the points {1,1,1}, {2,2,2}, … that make up the slice points.)
2 slices, 15 ways (removing 3 duplicates from the 18 total):
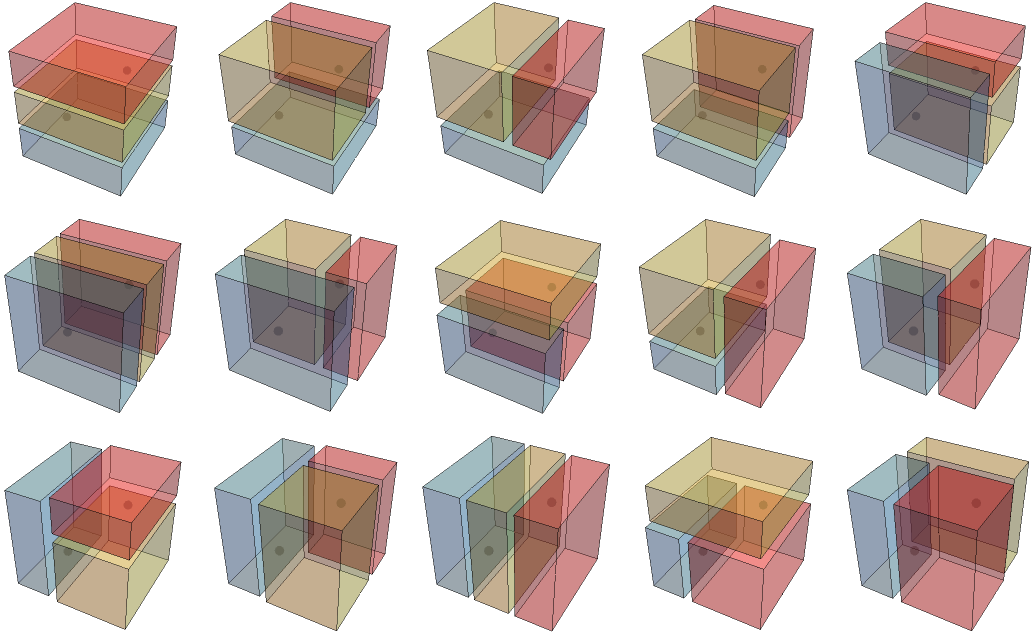
We’re counting as duplicates any figures with the same shape even though the cuts were in a different order.
3 slices, 93 ways (removing duplicates from the 162 total):

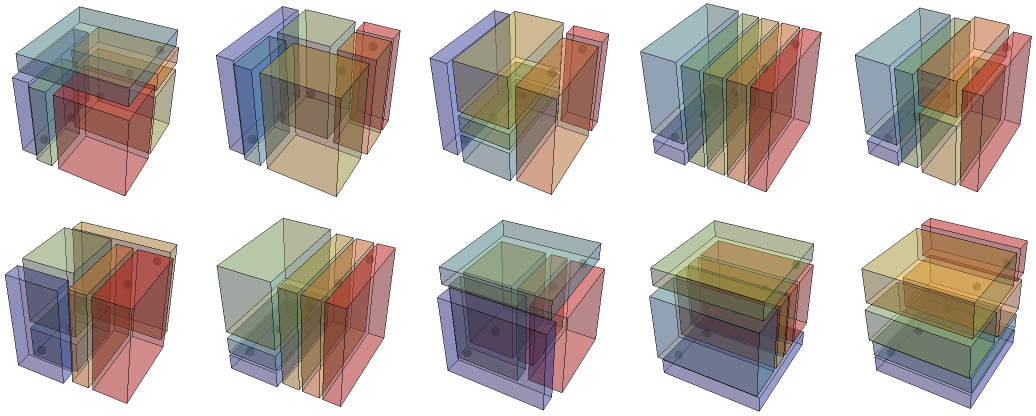
4 slices, 645 ways (removing duplicates from the 1,944 total):

After that, the counts are 4791, 37275, 299865, …, counted by OEIS sequence A103210.
A random selection of the 4,791 5-slices:
A random selection of the 32,275 6-slices:
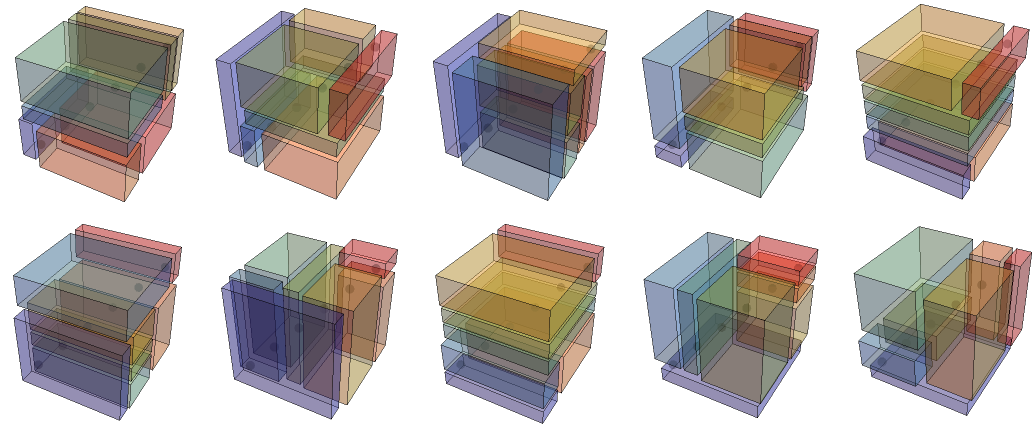
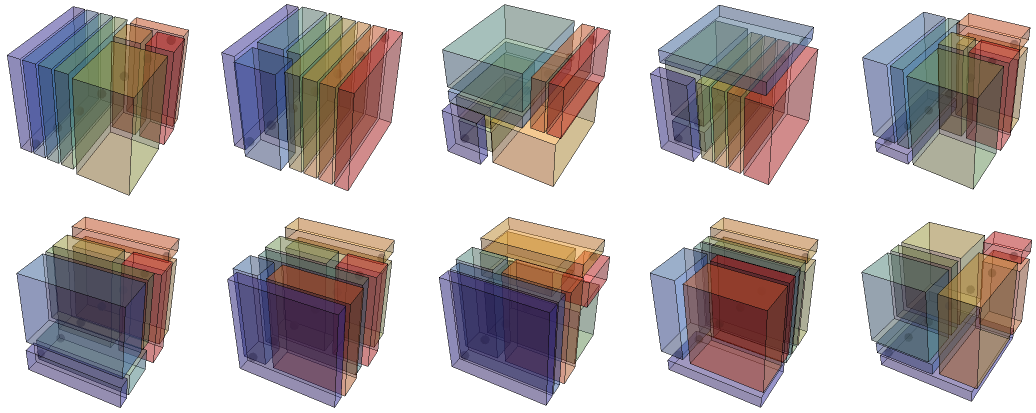
And a random selection of the 299,865 7-slices:
Designed and rendered using Wolfram Mathematica 13 and 14.
First draft September 2023 by Robert Dickau.
[ home ] || [ 2024-02-11 ]