Relatives of the Sierpinski Gasket

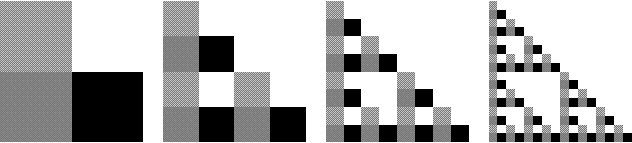
One of the many ways to generate the Sierpinski gasket is to begin with a “seed” such as an L-shape; make three copies of the seed and arrange them in an L-shape, and repeat the process an infinite (or at least sufficiently large) number of times.

Four iterations toward the Sierpinski gasket:

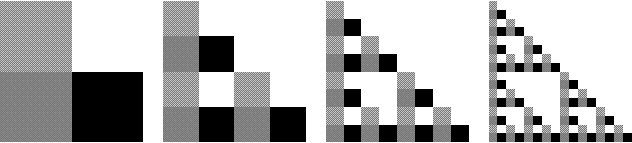
For other interesting variations, each of the three square “blocks” in the L-shape can be rotated or flipped, possibly with a different transformation for each square. The eight possible transformations of the seed are:

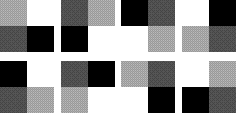
(In the Mathematica code I call the transformations Identity, MapReverseTranspose, ReverseMapReverse, ReverseTranspose, TransposeReverseMapReverse, Reverse, Transpose, MapReverse, not that you asked.)

To generate a picture, choose a transformation for the NW, SW, and SE quarters of the L-shape, and iterate the transformations. Two randomly selected pictures:

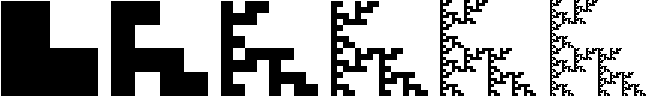
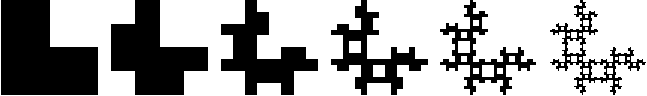
Taking every combination of transformations, and then removing duplicates, we find these 456 Sierpinski relatives:

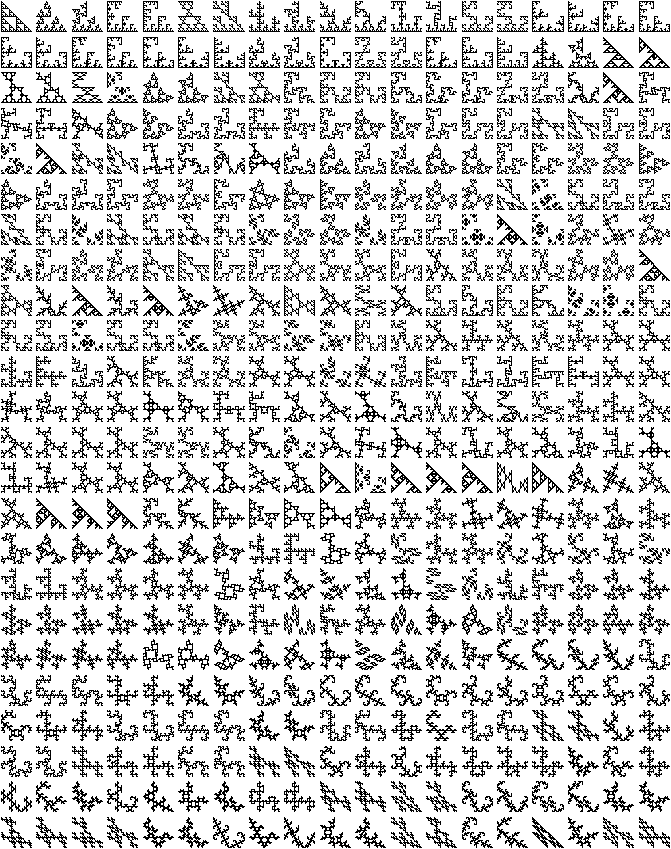
See Peitgen, Jürgens, and Saupe, Chaos and Fractals: New Frontiers of Science, Springer-Verlag, 1992; pp. 244–251.

Designed and rendered with Mathematica.

© 2001–2024 by Robert Dickau.

[ home ] || [ 2001-06-23 ]