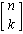
 ,
where the first is slightly easier to type.
,
where the first is slightly easier to type.The Stirling numbers of the first kind, or Stirling cycle numbers,
count the number of ways to permute a list of n items into
k cycles. Common notations are s(n, k) and
 ,
where the first is slightly easier to type.
,
where the first is slightly easier to type.
For example, the list {1, 2, 3, 4} can be permuted into two cycles in the following ways:
There are 11 such permutations, thus s(4, 2) = 11.
Here are some diagrams showing the cycles for permutations of a list with five elements.
s(5, 1) = 24, that is, all 5 elements form 1 cycle:
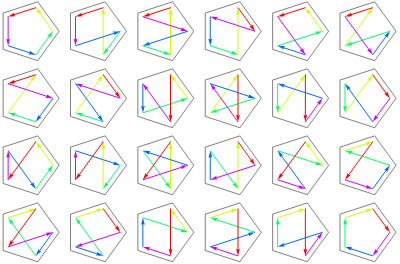
s(5, 2) = 50, meaning 5 elements form 2 cycles, where a dot is a cycle of length 1:

s(5, 3) = 35:
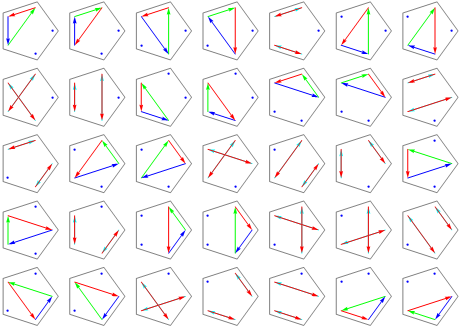
s(5, 4) = 10:

s(5, 5) = 1:
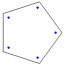
Designed and rendered using Mathematica 3.0 (for NeXT) and—much later—7.0 (for Windows).
© 1996–2025 by Robert Dickau.
[ home ] || [ 2010-12-29 ]