Sierpinski Tetrahedron

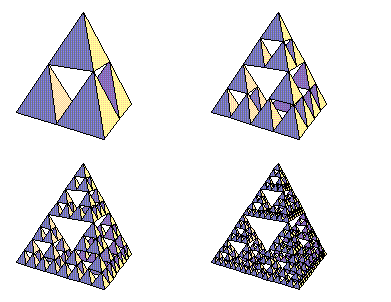
Starting with a simple tetrahedron, repeatedly place four tetrahedra with half the previous edge length at the four corners of the original. The result is an approximation to the Sierpinski tetrahedron, or tetrix.

Here’s the awful code that made this (I don’t condone programming this way — my excuse is that it was 3:15 a.m.):

(* for the KSubsets function, which seems like a huge waste *)

Needs["DiscreteMath`Combinatorica`"];

(* vertices of original tetrahedron, copied from Graphics`Polyhedra` *)

{v1, v2, v3, v4} =
    {{0, 0, 1.73205}, {0, 1.63299, -0.57735},
     {-1.41421, -0.816497, -0.57735}, {1.41421, -0.816497, -0.57735}};

(* midpoint function *)

mp[x1_, x2_] := 0.5 (x1 + x2);

(* maketet replaces a tetrahedron with four smaller ones --
    this would be better using Outer or some such thing *)

SetAttributes[maketet, Listable];

maketet[tet[{v1_, v2_, v3_, v4_}]] :=
    {tet[{v1, mp[v1,v2], mp[v1,v3], mp[v1,v4]}],
     tet[{v2, mp[v1,v2], mp[v2,v4], mp[v2,v3]}],
     tet[{v3, mp[v1,v3], mp[v3,v4], mp[v3,v2]}],
     tet[{v4, mp[v1,v4], mp[v2,v4], mp[v3,v4]}]};

(* makepolyrules creates the polygons that make up a tetrahedron ---
     if I were smart I'd create only the polygons visible from
     the viewer's viewpoint *)

makepolyrules =
	tet[{a_, b_, c_, d_}] ->
		With[{verts = KSubsets[{a,b,c,d}, 3]}, Map[Polygon, verts]];

Show[GraphicsArray[
    Partition[
      Graphics3D[#, Boxed->False, ViewPoint->{2.344, -2.386, 0.514}]&/@
          NestList[maketet, tet[{v1,v2,v3,v4}], 3] /. makepolyrules, 2]]];

Designed and rendered using Mathematica 2.2 and 3.0 for the Apple Macintosh.

[ home ] || [ 97???? ]