In 1968, Professor Gonzalo Vélez–Jahn (Universidad Central de Venezuela) discovered three-dimensional bodies with Möbius strip–like characteristics. Specifically, a trajectory along the cube faces behaves as if it were on a one-sided Möbius strip, in the sense that the end of the path will touch all of the polyhedron’s faces and eventually meet its beginning.
Martin Gardner later described these sorts of figures as prismatic rings and toroidal polyhedrons.
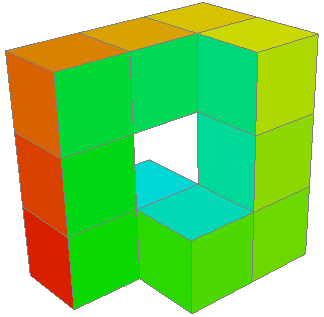
As a non-example, here’s a torus made of cubes.

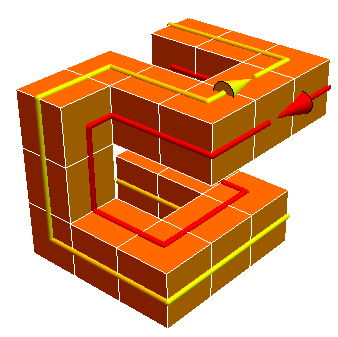
The figure has four faces (with two, plus a bit of a third, highlighted with arrows).
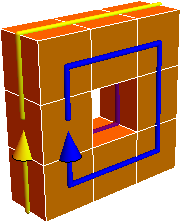
However, introducing various twists results in a figure with a single face, in the Möbius strip sense. Here’s a single-sided figure made of 10 cubes:
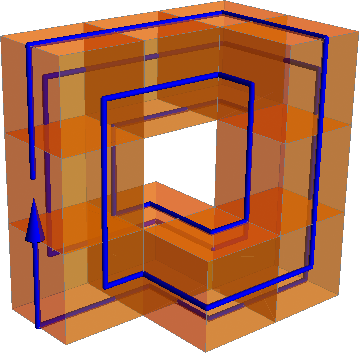
Or the same thing with a color gradient showing the path instead of an arrow:

When you slice through the cubes, you still have a connected figure:
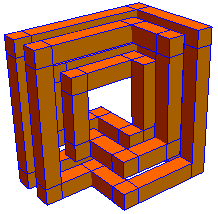
The sliced figure is also one-sided, as it turns out:

To run it into the ground, here’s a second slice:

And a third:
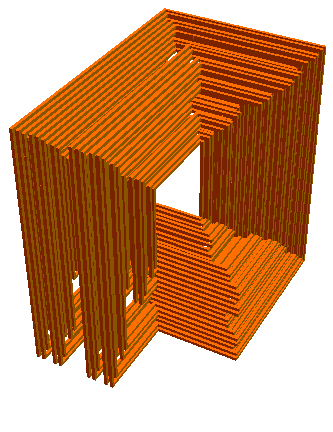
And a fourth:
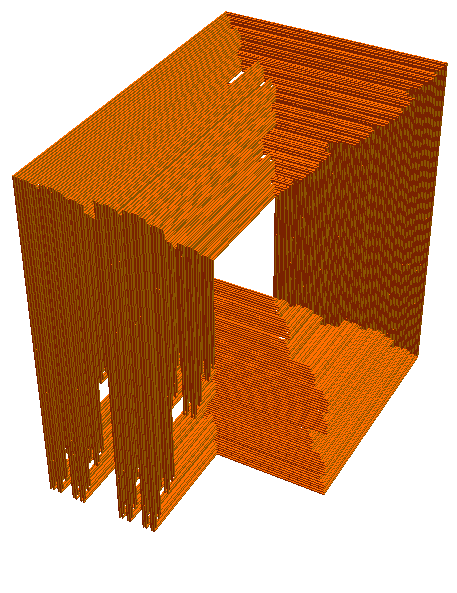
Funny enough, a slice through the figure parallel to one of the axes looks like Cantor dust.
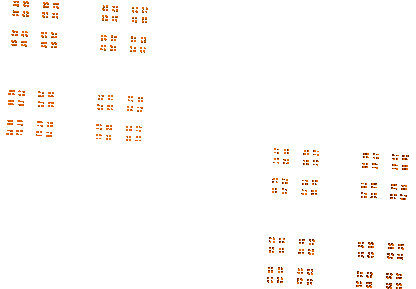
While we’re at it, a 22-cube single-sided figure:

Here it is, sliced:

By introducing more twists, we can create a two-sided figure:
Sliced. I’d hoped this would result in a disconnected figure, but nope:

Without whom not: Professor Gonzalo Vélez–Jahn, Luis Vélez, and Roger Bagula.
See Martin Gardner, Fractal Music, Hypercards and More…, pp. 81–86, 1992.
See also Moebius 3D Wiki [dead link 26-Dec-2021].
Figures created with Mathematica 10.
Robert Dickau, 2016.
[ home ] || [ 2016-04-24 ]
robertdickau.com/toroidalpolyhedra.html