Euler Zigzag Numbers

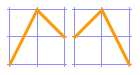
The numbers of alternating permutations (permutations in which the difference between each successive pair of adjacent elements changes sign—that is, each “rise” is followed by a “fall”, and vice versa) for n elements are sometimes called the Euler zigzag numbers. For the list {1, 2, 3}, the permutation {1, 3, 2} is an alternating permutation, while {3, 2, 1} is not. Determining the number of alternating permutations of the elements {1, 2, …, n} is called André’s Problem.

The following examples illustrate only the alternating permutations that begin with a “rise”; we can get all the permutations that begin with a “fall” by flipping the images vertically.

For the list {1, 2, 3}, there are 2 alternating permutations.

For {1, 2, 3, 4}, there are 5 alternating permutations.

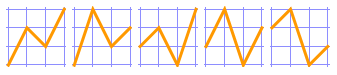
For {1, 2, 3, 4, 5}, there are 16 alternating permutations.

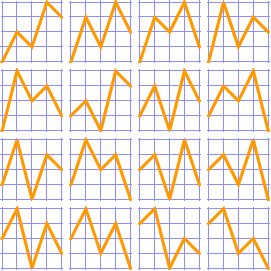
For {1, 2, 3, 4, 5, 6}, there are 61 alternating permutations.

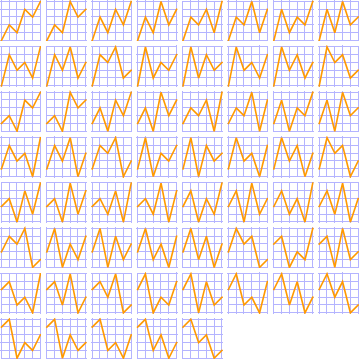
For {1, 2, 3, 4, 5, 6, 7}, there are 272 alternating permutations.

© 2000–2024 Robert Dickau.

[ home ] || [ 2001-01-01 ]