Create an equilateral triangle and choose a random point inside it, then repeatedly place a new point midway between the current point and one of the triangle’s corners (chosen randomly), and eventually (after throwing the first few points away) the points will look more and more like a Sierpinski triangle.
The following array shows progressively greater numbers of iterations of the preceding process, called the chaos game.
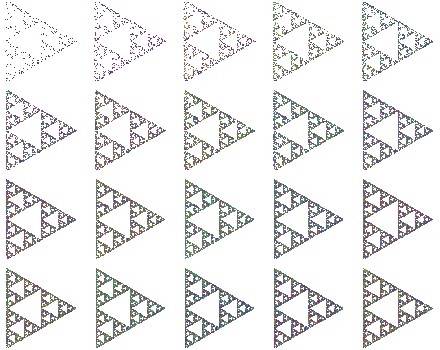
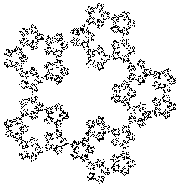
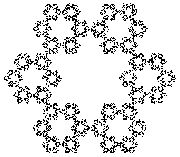
Interesting shapes also appear when starting with a shape other than a triangle and adjusting the fraction of the distance between the current point and the randomly chosen corner.
As it happens, starting with a tetrahedron instead of a triangle gives a similar tetrix-like result in three dimensions. In the following figure, each point is colored according to its distance from the observer’s viewpoint, not that it seems to help much.

Designed and rendered using Mathematica versions 2.2 and 3.0 for the Apple Macintosh.
© 1996–2026 by Robert Dickau
[ home ] || [ 2011-01-01 ]
www.robertdickau.com/chaos_game.html