One of the many interpretations of the Catalan numbers Cn is that they count the number of noncrossing partitions of the set {1, 2, ..., n}. A non-crossing partition is a partition in which lines joining members of the same subset do not intersect any lines joining members of another subset.
One representation of noncrossing partitions is one in which points are arranged at the corners of a regular polygon, with line segments connecting members of the same block.
Two points, two non-crossing partitions {{1, 2}}—joined by a line since they’re in the same subset—and {{1}, {2}}—not joined since they’re in different subsets:
Three points, five non-crossing partitions ({{1, 2, 3}}, {{1,2},{3}}, {{1,3},{2}}, {{1},{2,3}}, and {{1},{2},{3}}):
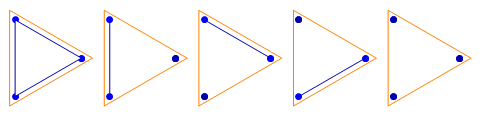
Four points, 14 non-crossing partitions:
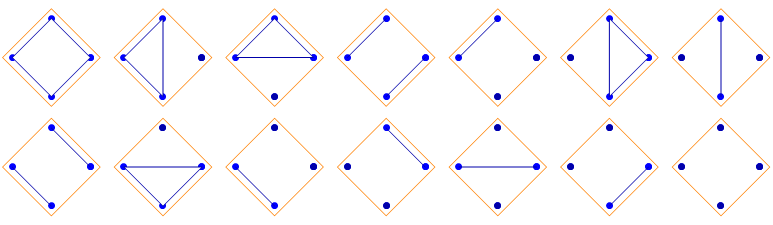
Five points, 42 non-crossing partitions:
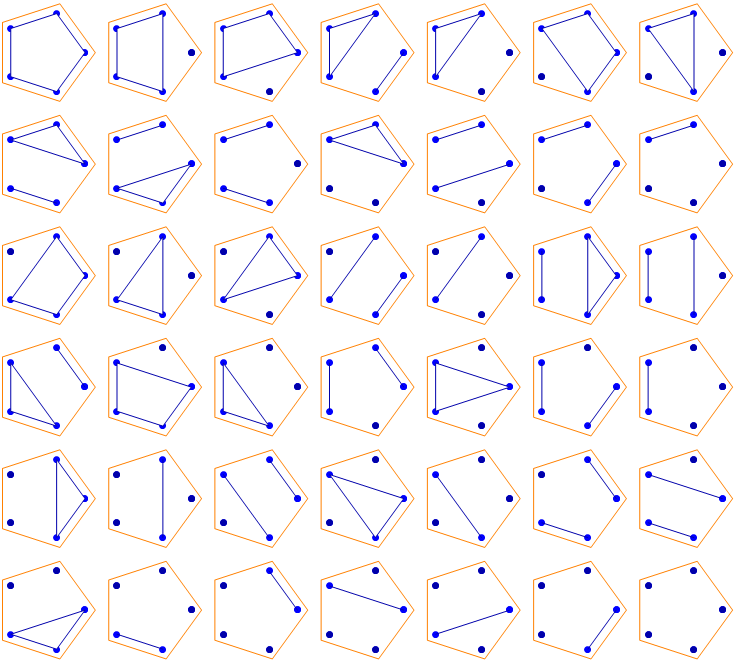
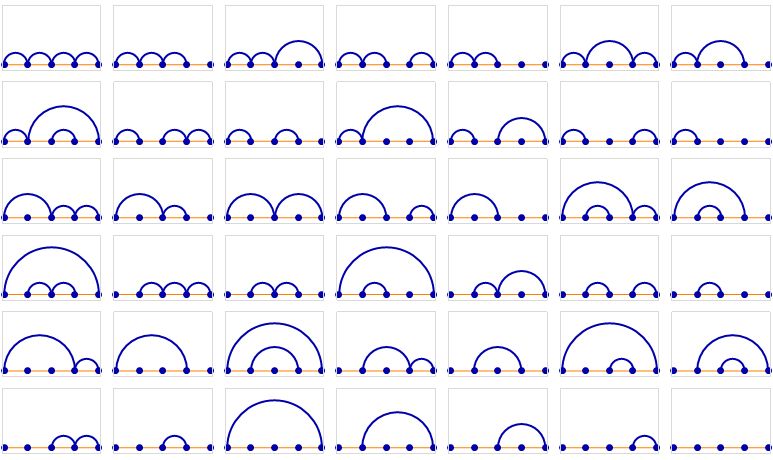
An equivalent representation is one in which points are arranged in a line, with arcs joining members of the same block.
Two points, two non-crossing partitions ({{1, 2}} and {{1}, {2}}, again):
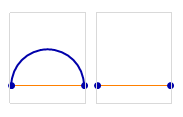
Three points, five non-crossing partitions ({{1, 2, 3}}, {{1,2},{3}}, {{1,3},{2}}, {{1},{2,3}}, and {{1},{2},{3}}):

Four points, 14 non-crossing partitions:
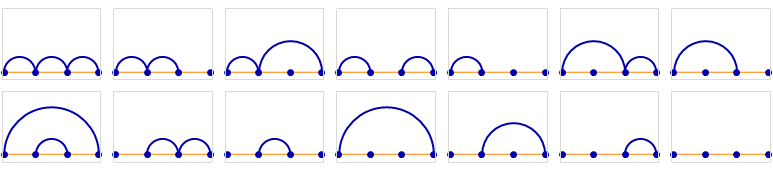
Five points, 42 non-crossing partitions:
© 2012–2026 by Robert Dickau.
[ home ] || [ 2012-04-22 ]