Sierpinski Arrowhead Curve (and friends)

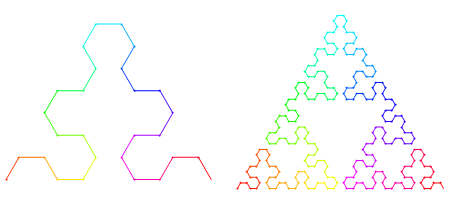
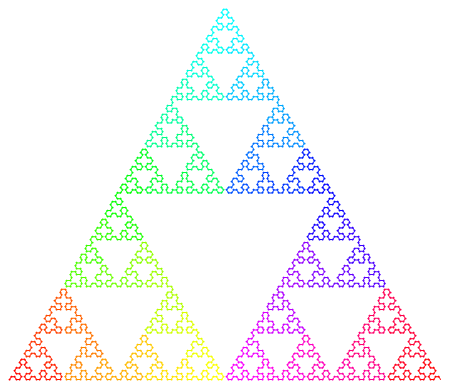
The Sierpinski arrowhead curve is a fractal curve that eventually coincides with the Sierpinski sieve, which seems to pop up everywhere. The Sierpinski arrowhead curve can be described by an L-system.

iterations 2 and 4
iteration 6

Just as the Hilbert and Moore curves are related, the Sierpinski arrowhead curve—where the start and end points are adjacent corners of the bounding triangle—has a relative (unnamed, as far as I can tell) where the start and end points are next to each other (see bottom center of each figure):

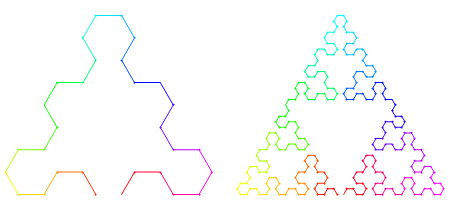
iterations 2 and 4 of arrowhead variation
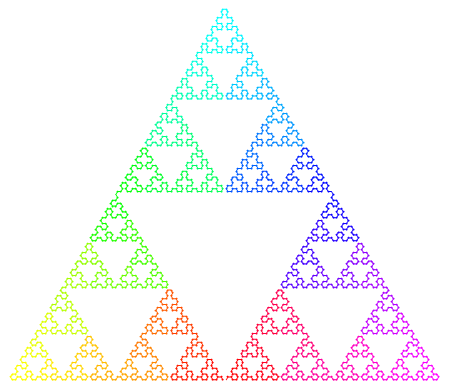
iteration 6 of variant

And just as the 2D versions of the Hilbert, Moore, Lebesgue, and other curves can be extended to three dimensions, the Sierpinski arrowhead curve can be extended to 3D to approximate the tetrix or Sierpinski tetrahedron. Here’s one way to do it:

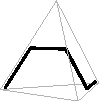
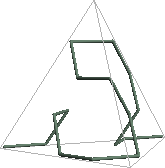
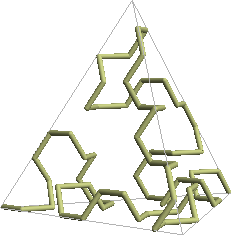
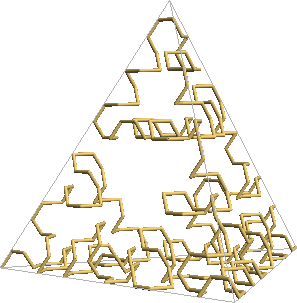
seed of 3D arrowhead curve iteration 1 of 3D arrowhead curve iteration 2 iteration 3 iteration 4 iteration 5 iteration 6

[ home ] || [ 2018-07-20 ]